不偏分散の謎に迫る（３）〜n-1で割る理由に迫る〜

株式会社神戸デジタル・ラボ　DataIntelligenceチームの高木です。

前回の記事では、このシリーズのメインである不偏分散について解説しました。本記事では、不偏分散を数式の観点から見ていき、「なぜn-1で割るのか？」という疑問を解決していきます。

この記事は全3記事にわたるシリーズの最終記事（3記事目）になります。

不偏分散の謎に迫る（１）〜分散を理解し、不偏分散の存在を知る〜
　データのばらつきを知ることができる分散の基本を確認し、本シリーズのメインの不偏分散を理解するための前提知識を身につけます。
不偏分散の謎に迫る（２）〜不偏分散を理解する〜
　不偏分散そのものについて理解し、分散と不偏分散の違いを踏まえた適切な使い分けができることを目指します。
不偏分散の謎に迫る（３）〜n-1で割る理由に迫る〜
　分散と不偏分散において、一般式の違いが生まれる理由を数式を利用して解き明かします。

0章全体概要
1章期待値
- 確率変数
- 期待値
2章推定量の性質
- 定性的理解
- 数式的理解
  - 一致性
  - 不偏性
3章標本数が1の時の期待値と分散
4章母平均の推定量
5章母分散の推定量
6章まとめ

本記事では、期待値、推定量における数式的理解、標本数が1の時の期待値と分散といった前提知識について解説し、母平均と母分散の推定量について数学的に考えるという流れで進めることにします。

0章全体概要

本シリーズのメインである不偏分散は、以下のような式で表すことができました。

$\text{不偏分散}　=　\dfrac{1}{n - 1} \displaystyle \sum_{i=1}^{n}\left( x_i - \bar{x} \right)^{2}$

シリーズの最後である今回は、「なぜn-1で割るのか？」を深く掘り下げていきます。記事の構成としては、以下の通りです。

本内容を理解するために、1章から3章までは必要な前提知識の解説を行います。具体的には、以下の通りです。

【1章】期待値
統計分野でよく利用される専門用語である期待値を、具体例を用いながら解説します。
【2章】推定量の性質
前回の記事で解説した推定量について、数学的な観点から考察します。
【3章】標本数が1の時の期待値と分散
母集団に対しての標本数が1という特殊な場合においての、期待値と分散を理解します。

前提知識を獲得した後は、メインである分散を取り扱う前に、比較的計算が簡易な平均でシミュレーションを行います。
【4章】母平均の推定量
母集団の平均の推定量として、標本平均が利用できることを数式で解き明かします。

最後にメインである分散を取り扱い、 $n-1$ で割る理由について迫ります。
【5章】母分散の推定量
母集団の分散の推定量は、標本分散を $n-1$ で割った値である理由を数式で解き明かします。

1章期待値

この章では、以下のような当選金の宝くじを例にとって考えていきましょう！

等級	当選金	当選確率
1等	100,000円	1/10000
2等	50,000円	1/5000
3等	30,000円	1/1000
4等	10,000円	1/100

確率変数

任意の値をとるXがあって、それぞれの値に対して確率が対応しているときXを確率変数といいます。宝くじの例では、当選金が確率変数に該当します。

実は、前回までの記事で見てきた標本平均や、標本分散もこの確率変数に該当します。（標本は、母集団からランダムに抽出したものなので、平均や分散のそれぞれの値には確率が対応していると表現できるからです！）

期待値

1回の試行で得られる確率変数の平均値を期待値と定義します。

確率変数の平均値ということですので、確率変数に該当する標本平均や標本分散においても期待値を求めることが可能ということですね！

具体的な計算としては、確率変数と確率をかけあわせた値を合計します。

\begin{align} E[X] = \sum_{i=1}^{n} p_i x_i \end{align}

宝くじの例で、計算してみましょう！

$100,000 \times \dfrac {1} { 10000 } + 50,000 \times \dfrac {1} { 5000 } + 30,000 \times \dfrac {1} { 1000 } + 10,000 \times \dfrac {1} { 100 } = 150$

この計算結果は何をあらわしているのでしょうか？先程の定義を分解すると、

1回の試行：宝くじを買うという1回の行為
確率変数：宝くじの当選金

となるので、「宝くじを買うという1回の行為で得られる宝くじの当選金の平均」と言い換えることができますね！

つまり、先ほどの計算結果の150は「宝くじの当選金額の平均が150円である」ことを示しています。なかなか、良心的な宝くじですね（笑）

2章推定量の性質

定性的理解

前回の記事で、推定量は「一致性」と「不偏性」という持つべき2つの性質があることをご紹介しました。具体的な性質は以下の通りでしたね！

一致性：標本におけるサンプル数が大きくなればなるほど、推定量はだんだんと真の母集団のパラメータに近づくという性質

不偏性：標本数が多いほど、推定量はだんだんと真の母集団のパラメータに近づくという性質

今回は、これらの性質を数学的な観点から見ていきます！

数式的理解

一致性

【定義】

ある推定量が一致性をもつためには、以下の式が成立する必要があります。ここで、 $n$ は標本数、 ${\theta}$ は母数、 $\hat{\theta}$ は推定値、 $\epsilon$ は任意の限りなく小さい値、関数 $P$ は確率を表します。

\begin{align} \lim_{n \to \infty} P\left( |\hat{\theta} - {\theta}| - \epsilon \right) = 1 \end{align}

この数式は、標本数 $n$ を限りなく大きくすると、推定量 $\hat{\theta}$ は ${\theta}$ である確率が限りなく高くなることを示します。これは、先ほど紹介した定性的理解の性質とも一致しますよね！

【判断方法】

ある推定量が一致性を持つかどうかは以下の2条件の成立で判断できます。ここで、 $E$ は期待値、 $V$ は分散を表します。

\begin{align} \lim_{n \to \infty} E[\hat{\theta}] = \theta \end{align}

\begin{align} \lim_{n \to \infty} V[\hat{\theta}] = 0
\end{align}

それぞれの数式は、標本数 $n$ を限りなく大きくすると、 $\hat{\theta}$ の期待値は ${\theta}$ 、分散は 0 である確率が限りなく高くなることを表します。

不偏性

【定義】

ある推定量が不偏性をもつためには、以下の式が成立する必要があります。ここで、 ${\theta}$ は母数、 $\hat{\theta}$ は推定値を表します。

\begin{align} E[\hat{\theta}] = \theta \end{align}

この数式は、推定量 $\hat{\theta}$ は ${\theta}$ であることを示します。

一致性では、標本数 $n$ を限りなく大きくする必要がありましたが、不偏性ではその必要はありません。

3章標本数が1の時の期待値と分散

標本数が1といった特殊な場合を考えます。

この時、標本の分布は、母集団の分布と同一に従って、標本に対する期待値は母平均に等しく、標本における分散は母分散に等しいことが知られています。

こちらの情報は、後の計算で利用することになります！

4章母平均の推定量

前回の記事で、母平均に対しての推定量は、標本平均であることについて言及しました。

今回は、これを数式で証明していきます。一致性と不偏性について確認するために、まずは標本平均における期待値と分散を計算しましょう！

期待値

\begin{align} E[\bar{X}] &= E[\dfrac {1} { n } \left( X_1 + X_2 + \cdots + X_n \right)] \\ &= \dfrac {1} { n } E[\left( X_1 + X_2 + \cdots + X_n \right)] \\ &= \dfrac {1} { n } \left(E[X_1] + E[X_2] + \cdots + E[X_n] \right) \\ &= \dfrac {1} { n } \left(\mu + \mu + \cdots + \mu \right) \\ &= \dfrac {1} { n } \times n \mu \\ &= \mu \end{align}

以下の展開は、先程ご紹介した標本数が1の時の期待値は母平均に等しいという性質を利用しています！

\begin{align} E[X_i] = \mu \qquad i = 1, 2, \cdots , n\\ \end{align}

分散

\begin{align} V[\bar{X}] &= V[\dfrac {1} { n } \left( X_1 + X_2 + \cdots + X_n \right)] \\ &= \dfrac {1} { n^{2} } V[\left( X_1 + X_2 + \cdots + X_n \right)] \\ &= \dfrac {1} { n^{2} } \left(V[X_1] + V[X_2] + \cdots + V[X_n] \right) \\ &= \dfrac {1} { n^{2} } \left(\sigma^{2} + \sigma^{2} + \cdots + \sigma^{2} \right) \\ &= \dfrac {1} { n^{2} } \times n \sigma^{2} \\ &= \dfrac {\sigma^{2}} { n } \end{align}

以下の展開は、先程ご紹介した標本数が1の時の分散は母分散に等しいという性質を利用しています！

\begin{align} V[X_i] = \sigma^{2} \qquad i = 1, 2, \cdots , n\\ \end{align}

一致性・不偏性

期待値・分散の情報を利用して、標本平均が推定量の性質を満たすかを確認しましょう！

【一致性】

\begin{align} \lim_{n \to \infty} E[X_i] \\ \end{align}

\begin{align} &= \lim_{n \to \infty} \mu \\ &= \mu \end{align}

\begin{align} \lim_{n \to \infty} V[X_i] \\ \end{align}

\begin{align} &= \lim_{n \to \infty} \dfrac {\sigma^{2}} { n } \\ &= 0 \end{align}

【不偏性】

\begin{align} E[X_i] = \mu \\ \end{align}

一致性を持つ2条件の式を満たし、不偏性も満たしているので、これで母平均に対しての推定量は、標本平均であることが確認できましたね！さあ、次は今回のシリーズのメインである分散を取り扱っていきましょう！

5章母分散の推定量

前回の記事で、母分散に対しての推定量に、標本分散を利用できず、標本分散に対してn-1で割った値が該当することについて言及しました。

このことを数式で理解してみましょう！具体的には、標本分散の期待値を計算して母分散に一致するかを確認してみることにします！

標本分散

\begin{align} \dfrac {1} { n }\sum_{i=1}^{n}\left( x_i - \bar{x} \right)^{2} = E[\dfrac {1} { n } \lbrace \left( X_1 - \bar{X} \right)^{2} + \cdots + \left( X_n - \bar{X} \right)^{2} \rbrace] \\ \end{align}

標本分散の期待値

標本分散の期待値を求めるために、母分散の定義の式変形を行います。

\begin{align} \sigma^{2} &= E[\dfrac {1} { n } \lbrace \left( X_1 - \mu \right)^{2} + \cdots + \left( X_n - \mu \right)^{2} \rbrace] \\ &= E[\dfrac {1} { n } \lbrace \left( X_1 - \bar{X} + \bar{X} - \mu \right)^{2} + \cdots + \left( X_n - \bar{X} + \bar{X} - \mu \right)^{2} \rbrace] \tag{1.1} \\ &= E[\dfrac {1} { n } \lbrace \left( X_1 - \bar{X} \right)^{2} + \cdots + \left( X_n - \bar{X} \right)^{2} \rbrace \\ & \qquad + \dfrac {1} { n } \lbrace 2\left( X_1- \bar{X} \right)\left( \bar{X} - \mu \right) + \cdots + 2\left( X_n- \bar{X} \right)\left( \bar{X} - \mu \right) \rbrace \\ & \qquad + \dfrac {1} { n } \lbrace \left( \bar{X} - \mu \right)^{2} + \cdots + \left( \bar{X} - \mu\right)^{2} \rbrace ] \tag{1.2} \\ &= E[\dfrac {1} { n } \lbrace \left( X_1 - \bar{X} \right)^{2} + \cdots + \left( X_n - \bar{X} \right)^{2} \rbrace \\ & \qquad + \dfrac {2} { n } \left( \bar{X} - \mu \right) \lbrace \left( X_1- \bar{X} \right) + \cdots + \left( X_n- \bar{X} \right) \rbrace \\ & \qquad + \dfrac {1} { n } \lbrace \left( \bar{X} - \mu \right)^{2} + \cdots + \left( \bar{X} - \mu\right)^{2} \rbrace ] \tag{1.3} \\ &= E[\dfrac {1} { n } \lbrace \left( X_1 - \bar{X} \right)^{2} + \cdots + \left( X_n - \bar{X} \right)^{2} \rbrace] \\ & \qquad + E[\dfrac {1} { n } \lbrace \left( \bar{X} - \mu \right)^{2} + \cdots + \left( \bar{X} - \mu\right)^{2} \rbrace] \tag{1.4} \\ &= E[\dfrac {1} { n } \lbrace \left( X_1 - \bar{X} \right)^{2} + \cdots + \left( X_n - \bar{X} \right)^{2} \rbrace] + \dfrac {\sigma^{2}} { n } \end{align}

このように変形すると右辺に標本分散が現れるので、両辺を入れ替えて、 \begin{align} E[\dfrac {1} { n } \lbrace \left( X_1 - \bar{X} \right)^{2} + \cdots + \left( X_n - \bar{X} \right)^{2} \rbrace] &= \dfrac {\sigma^{2}} { n } - {\sigma^{2}} \\ &= \dfrac {n-1} { n } {\sigma^{2}} \tag{2} \end{align}

これで、標本分散の期待値を求めることができました。

標本分散が推定量であるといえる場合、不偏性の性質より母分散に一致するはずですが、今回はしていません。よって、標本分散は推定量の条件を満たさないといえます。

【数式変換参考】

母分散の定義の式変形において少し難しい変形についての解説を行います。

式(1.3)から式(1.4)の変形において、 $\dfrac {2} { n } \left( \bar{X} - \mu \right)\lbrace \left( X_1- \bar{X} \right) + \cdots + \left( X_n- \bar{X} \right) \rbrace$ の項が消失していますが、これは初回の記事で扱った $\lbrace \left( X_1- \bar{X} \right) + \cdots + \left( X_n- \bar{X} \right) \rbrace = 0$ （平均からの偏差の合計は0）という特徴を利用しています。

不偏分散はなぜn-1で割るのか？

式(2)の両辺に対して、 $\dfrac {n} { n - 1}$ を掛け合わせると、

\begin{align} E[\dfrac {1} { n - 1 } \lbrace \left( X_1 - \bar{X} \right)^{2} + \cdots + \left( X_n - \bar{X} \right)^{2} \rbrace] &= \sigma^{2} \tag{3}\\ \end{align}

となります。

式(3)では $\dfrac {1} { n - 1 } \lbrace \left( X_1 - \bar{X} \right)^{2} + \cdots + \left( X_n - \bar{X} \right)^{2} \rbrace$ の期待値が、母分散の $\sigma^{2}$ になっているので母分散に対しての推定量の不偏性を満たしているということができます。

また、 $\dfrac {1} { n - 1 } \lbrace \left( X_1 - \bar{X} \right)^{2} + \cdots + \left( X_n - \bar{X} \right)^{2} \rbrace$ は、

式(2)の左辺である標本の分散 $\dfrac{1}{n} \displaystyle \sum_{i=1}^{n}\left( x_i - \bar{x} \right)^{2}$ に対して、

$\dfrac {n} { n - 1 }$ を掛けた値であるので $\dfrac{1}{n - 1} \displaystyle \sum_{i=1}^{n}\left( x_i - \bar{x} \right)^{2}$ とも表現できます。

以上をまとめると、 $\dfrac{1}{n - 1} \displaystyle \sum_{i=1}^{n}\left( x_i - \bar{x} \right)^{2}$ は推定量の候補と言えます。なぜ、ここで候補という言い方をしているかというと、不偏性は確認できていますが、一致性を確認できていないからです！

確認するためには、先程の平均の推定量の時と同様に一致性を持つために必要な2条件の式を満たしているかどうかで判別します。分散の計算が少し複雑ですので尺の都合上、確認を省略しますが、計算するとどちらの条件も満たすことになり、一致性を持つことがわかります。

これで、 $\dfrac{1}{n - 1} \displaystyle \sum_{i=1}^{n}\left( x_i - \bar{x} \right)^{2}$ は一致性も不偏性も満たすので、母分散に対する推定量であると言えますね！

この記事のメインテーマは「なぜn-1で割るのか？」でしたが、上記の式を求めるまでの過程がその答えになります。なかなか、複雑な計算でしたね！

おまけ

ここまで数式の証明によって「なぜn-1で割るのか？」を見てきましたが、自由度という観点からの考え方をおまけとしてご紹介します。

自由度とは、値を自由に決定できるデータの数のことです。例えば標本数が $n$ の時は、自由度が $n$ ということができます。

標本分散は $\dfrac{1}{n} \displaystyle \sum_{i=1}^{n}\left( x_i - \bar{x} \right)^{2}$ で表すことができました。上記の計算の中で $\bar{x}$ を利用しているのは、母平均の $\mu$ が標本の情報だけでは不明だからです。実は、この標本平均の $\bar{x}$ で計算しているということが自由度において問題になります。

母集団から標本数 $n$ の標本を抽出する際、本来の自由度は $n$ になる、すなわち、 $n$ 個のデータを自由に決定できるはずです。しかし、これが標本平均が $\bar{x}$ である場合どうなるでしょうか？

この場合、 $n-1$ 個のデータは母集団から自由に選択できますが、最後の1個は平均が $\bar{x}$ になるようなデータを選択しなければなりません。すなわち、自由度が $n-1$ になるわけです。これが $n-1$ で割る理由になります！

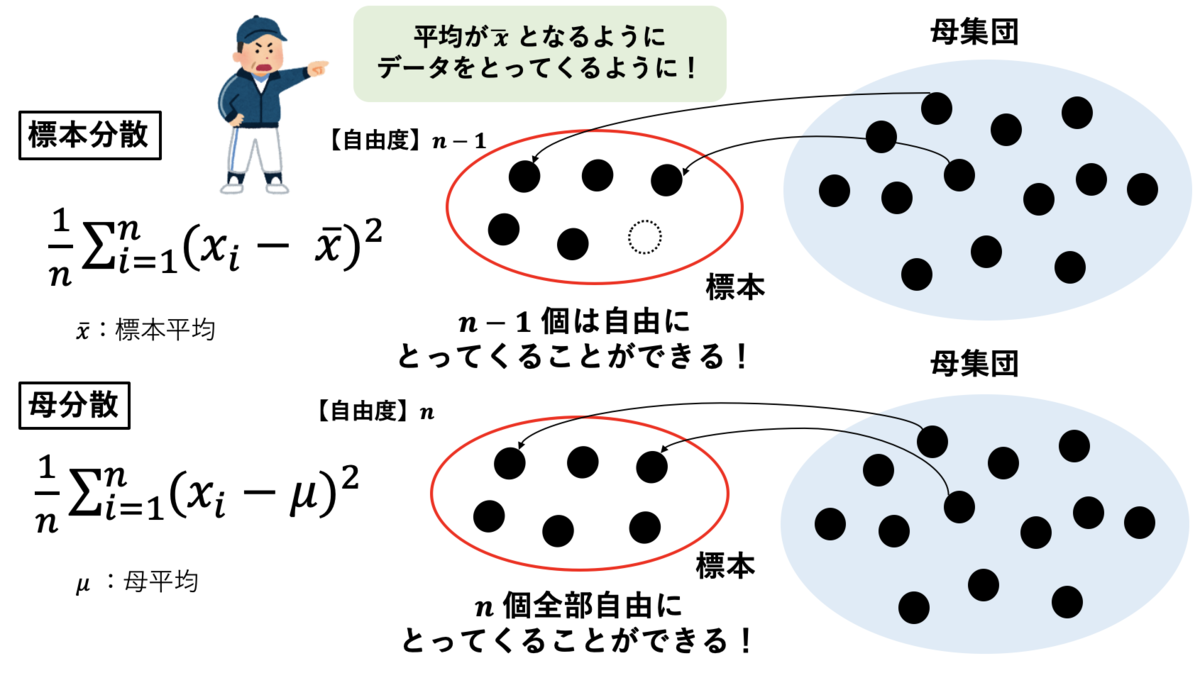
このように自由度を利用しても、「なぜn-1で割るのか？」ということは理解できます。同一のものを複数の観点から考える大切さを思い知らされますね！

6章まとめ

この不偏分散の謎に迫るシリーズでは、初回の記事の「そもそも分散って何？」から、順を追って解説し、シリーズ最後にあたる本記事では「不偏分散はなぜn-1で割るのか？」という疑問を数式を使って解き明かしていきました。

今回のシリーズで扱ったテーマは、統計学の中でも特に記述統計学と呼ばれる分野の基本になります！「これが基本なのか！！」と思われる方もいらっしゃるかもしれませんが、何事も基本が一番難しいものです。

このシリーズを通して、皆さんにとって統計学が身近なものとなり、さらなる勉強のきっかけとなれば嬉しいです。

高木裕仁

データインテリジェンスチーム所属
データサイエンティスト。自然言語処理を中心としながら、その他の非構造化データや構造化データに関しても偏りなく扱います。こちらのブログでは、自然言語処理に関するトピックやAzureを中心としたクラウドを利用したデータ活用に関してのトピックを中心に様々な記事を発信していきます。

神戸のデータ活用塾！KDL Data Blog

KDLが誇るデータ活用のプロフェッショナル達が書き連ねるブログです。